A. Notes
A path between two vertices in a graph is a list of vertices, in which successive vertices are connected by edges in the graph.
The length of a path is the number of edges on the path.
A simple path is a path with no vertex repeated.
A graph is connected if if there is a path from every vertex to every other vertex in the graph.
A graph is traversable if you can draw a path (not simple path) covering all the vertices without retracing any edge. Obviously, a traversable graph is connected.
B. HW
1. In the graph below, how many paths can you find from A to D? Is this graph connected?
How many simple paths from A to F are there? Is this graph traversable?
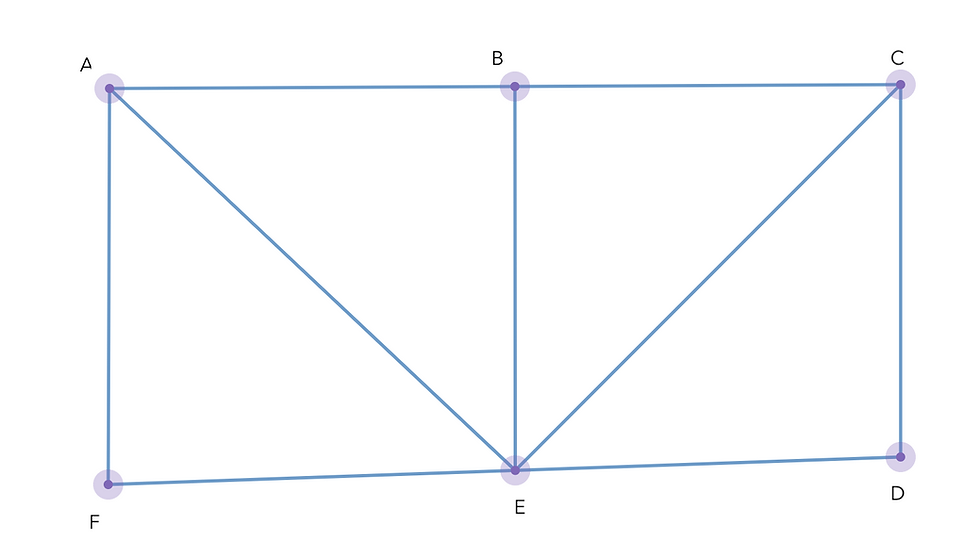
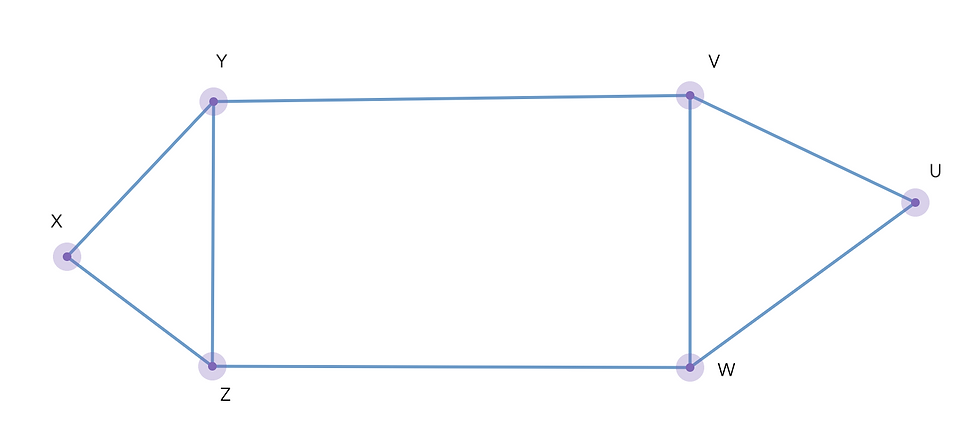
2. In the graph below, what is the longest simple path? Is this graph traversable? If you can add an edge, can you make the graph traversable?

10, no, 5, no
vuwzxy, no, no
10, no, 5, no
v u w z x y, no, no